Vector Control Of Induction Motor

Three-phase AC induction motors (ACIM) are popular in industry for a number of reasons. Their construction is extremely optimized, since they have been produced for years. They are very simple and manufacturing costs are favorable. They have no brushes and require minimum maintenance. The robustness of the motor is another strong advantage. We would find induction motors mostly in applications such as water pumps, compressors, fans and air-conditioning systems.

In order to achieve variable speed operations in a three-phase AC induction motor, a variable voltage and variable frequency needs to be supplied to the motor. Modern three-phase variable speed drives (VSD) are supplied with digitally controlled switching inverters.

The control algorithms can be sorted into two general groups. The first group is referred to scalar control. The constant Volt per Hertz control is a very popular technique representing scalar control. The other group is called vector or field oriented control (FOC). The vector oriented techniques brings overall improvements in drive performance over scalar control. Let’s mention the higher efficiency, full torque control, decoupled control of flux and torque, improved dynamics, etc.

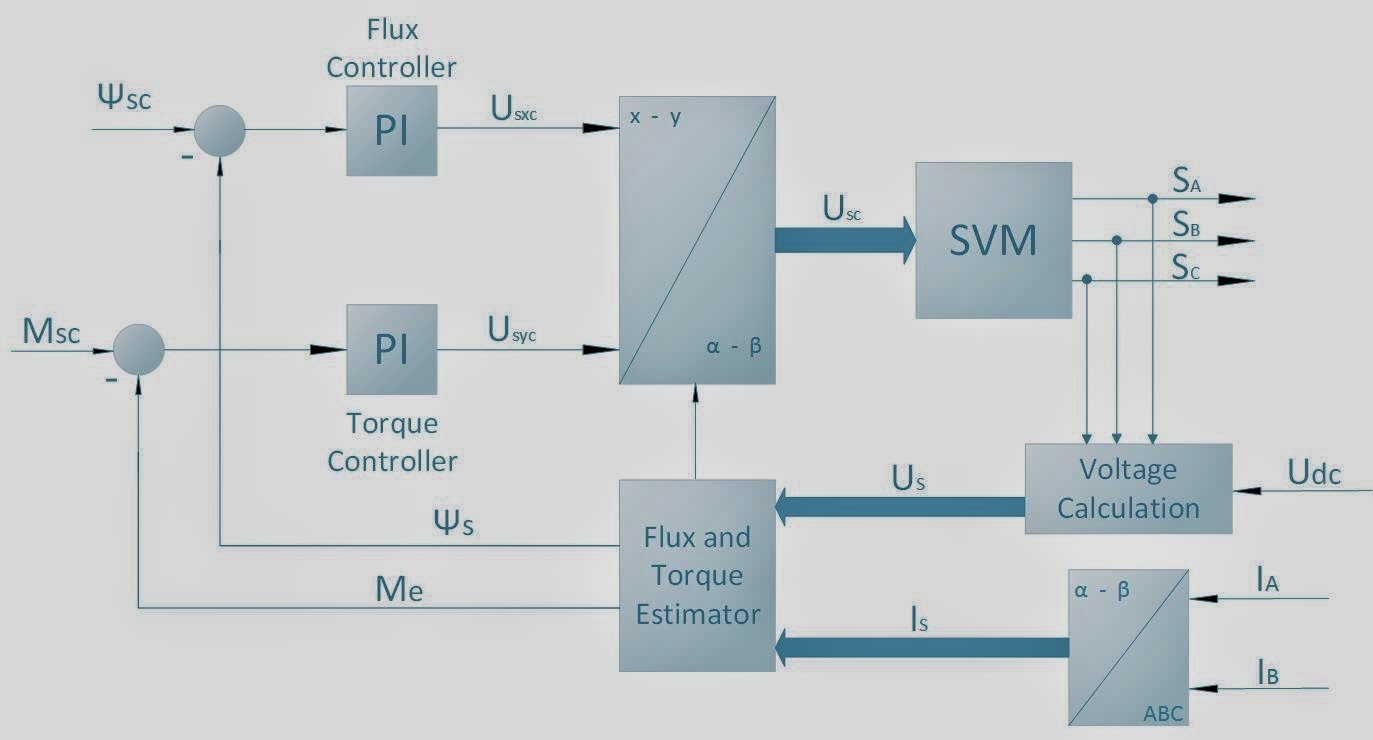
Fundamental Principle of Vector Control

            High-performance motor control is characterized by smooth rotation over the entire speed range of the motor, full torque control at zero speed, fast accelerations and deceleration. To achieve such control, vector control techniques are used for three-phase AC motors. The basic idea of the vector control algorithm is to decompose a stator current into flux and torque producing components. Both components can be controlled separately after decomposition. The structure of the motor controller is then as simple as that for a separately excited DC motor. Figure shows the basic structure of the vector control algorithm for the AC induction motor. To perform vector control, it is necessary to follow these steps:

1.  Measure the motor quantities (phase voltages and currents)
2.   Transform them into the 2-phase system (α,β) using a Clarke transformation
3.  Calculate the rotor flux space-vector magnitude and position angle
4.   Compare this with reference flux and torque by using PI controller.
5.  The PI controller output is again converted to Clarke transformation and given to the SVM.